Si hacemos coincidir el centro de una circunferencia de radio unidad con el origen de coordenadas obtenemos la circunferencia trigonométrica (también llamada circunferencia goniométrica), en la que el seno y el coseno de un ángulo vienen representados por la ordenada y por la abscisa, respectivamente.
La circunferencia trigonométrica es una circunferencia de radio unidad en la que se inscriben los ángulos, con el vértice en su centro. También en su centro se ubica el origen de un sistema de coordenadas ortogonales (x, y). En la circunferencia trigonométrica se considera que los ángulos están orientados; se atribuye un signo al sentido de giro: si los ángulos se miden desde el eje x, crecen positivamente en sentido contrario al de las agujas del reloj. Por lo tanto, si se miden en sentido horario, los ángulos serán negativos.
La razón del valor uno es por simple comodidad, es mas fácil deducir los valores de las funciones trigonométricas a partir de un valor simple como uno (el único valor más simple que 1 es cero, pero el cero no aplica en este caso), así que se toma este por hacer las cosas mas fáciles y poder deducir los valores de manera sencilla.
La circunferencia trigonométrica es una circunferencia de radio unidad en la que se inscriben los ángulos, con el vértice en su centro. También en su centro se ubica el origen de un sistema de coordenadas ortogonales (x, y). En la circunferencia trigonométrica se considera que los ángulos están orientados; se atribuye un signo al sentido de giro: si los ángulos se miden desde el eje x, crecen positivamente en sentido contrario al de las agujas del reloj. Por lo tanto, si se miden en sentido horario, los ángulos serán negativos.
La razón del valor uno es por simple comodidad, es mas fácil deducir los valores de las funciones trigonométricas a partir de un valor simple como uno (el único valor más simple que 1 es cero, pero el cero no aplica en este caso), así que se toma este por hacer las cosas mas fáciles y poder deducir los valores de manera sencilla.
Si (x, y) es un punto de la circunferencia unidad, y el radio que tiene el origen en (0, 0), forma un ángulo 
con el eje X, las principales funciones trigonométricas se puede definir como valores de segmentos asociados a triangulos rectangulos auxiliares, de la siguiente manera:
con el eje X, las principales funciones trigonométricas se puede definir como valores de segmentos asociados a triangulos rectangulos auxiliares, de la siguiente manera:
y dado que la hipotenusa es igual al radio, que tiene valor = 1, se deduce:
El coseno es la razón entre el cateto adyacente y la hipotenusa:
y como la hipotenusa tiene valor = 1, se deduce:
La tangente es la razón entre el cateto opuesto y el cateto adyacente:
A continuacion esta la grafica de los angulos mas comunes y las coordenadas sobre la circunferencia trigonometrica:
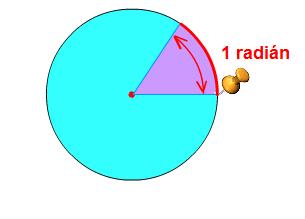
Radian: Representa el ángulo central en una circunferencia que subtiende un arco cuya longitud es igual a la del radio. Su símbolo es rad. A continuacion con la siguiente grafica la teoria sera mucho mas facil de entender:
Para convertir de grados a radianes, el valor dado en grados debe ser multiplicado por π y dividido para 180 grados. Ejemplo
Pasar 150 grados a radianes:
150°× π/180° = 2.62 rad
Para convertir de grados a radianes, el valor dado en radianes debe ser multiplicado por 180 grados y dividido para π. Ejemplo
Pasar 0.5rad a grados:
0.5rad × 180°/π = 28.65°
